Skip lists are a fascinating data structure: very simple, and yet have the same asymptotic efficiency as much more complicated AVL trees and red-black trees. While many standard libraries for various programming languages provide a sorted set data structure, there are numerous problems that require more control over the internal data structure than a sorted set exposes. In this article, I will discuss the asymptotic efficiency of operations on skip lists, the ideas that make them work, and their interesting use cases. And, of course, I will give you the source code for a skip list in C#.
The time complexity of basic operations on a skip list is as follows:
| Operation | Time Complexity |
| Insertion | O(log N) |
| Removal | O(log N) |
| Check if contains | O(log N) |
| Enumerate in order | O(N) |
This makes skip list a very useful data structure. First, as mentioned earlier, skip list can be used as the underlying storage for a sorted set data structure. But, skip list can be directly used to implement some operations that are not efficient on a typical sorted set:
- Find the element in the set that is closest to some given value, in O(log N) time.
- Find the k-th largest element in the set, in O(log N) time. Requires a simple augmentation of the the skip list with partial counts.
- Count the number of elements in the set whose values fall into a given range, in O(log N) time. Also requires a simple augmentation of the skip list.
From a singly-linked list to a skip list
Sometimes the best way to understand how something works is to attempt to design it yourself. Let’s try to go through that exercise with skip lists.
First, consider a regular sorted singly-linked list. Here is an example of one:
A sorted singly-linked list is not a terribly interesting data structure. The complexity of basic operations looks like this:
| Operation | Time Complexity |
| Insertion | O(N) |
| Removal | O(N) |
| Check if contains | O(N) |
| Enumerate in order | O(N) |
That is pretty unimpressive, actually. The only interesting value here is the O(N) in-order enumeration. For an insertion, removal or search, O(N) is about as bad as it gets. (There are more specialized use cases where sorted linked lists are appropriate, though.)
So, how can we make these operations on a sorted linked list faster? The main problem with a linked list is that it takes so long to get into its middle. That makes insertion, removal and search operations all O(N).
Well, here is an idea: let’s consider a sorted multi-level list. We start out with a regular singly-linked list that connects nodes in-order. Then, we add a level-2 list that skips every other node. And a level-3 list that skips every other node in the level-2 list. And so forth, until we have a list that jumps somewhere past the middle element. Our previous list now looks like this:
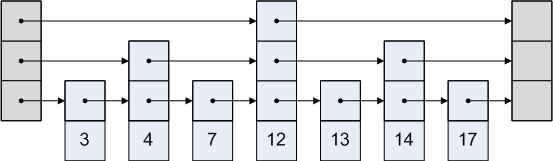
Now, checking whether a particular element is in the set only takes O(log N). The search algorithm is a lot like binary search. We first look in the top-most list and move to the right, making sure that we don’t jump too far. For example, if we are searching for number 8, we will not take the level-3 link from the head node, because we would end up too far right: all the way at 12! If we can’t move further right on a particular level, we drop to the next lower level, which has shorter jumps.
Search for value 8 would proceed like this:
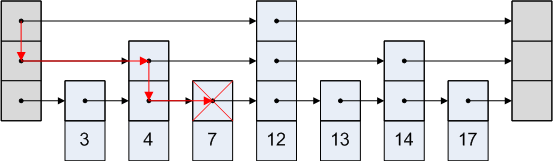
Since we landed on a 7, but we were looking for an 8, that means that 8 is not in the set.
The O(log N) search time is very nice. But, there is a problem: how do we implement insertions and removals efficiently, but in a way so that they maintain the structure of the multi-level list? This turns out to be quite a problem. AVL and red-black trees resolve it by tricky rebalancing operations.
Skip lists take an entirely different approach: a probabilistic one. Instead of ensuring that the level-2 list skips every other node, a skip list is designed in a way that the level-2 list skips one node on average. In some places, it may skip two nodes, and in other places, it may not skip any nodes. But overall, the structure of a skip list is very similar to the structure of a sorted multi-level list.
Here is an example of what a skip list may look like:
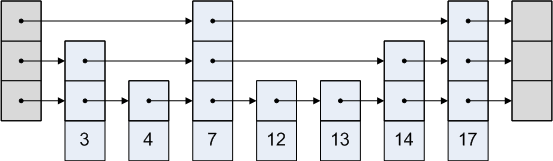
A skip list looks a bit like a slightly garbled sorted multi-level list. A skip list has many of the nice properties of a sorted multi-level list, such as O(log N) search times, but also allows simple O(log N) insertions and deletions.
Implementation of skip lists
So, given this description of a skip list, would you know how to implement it? It is not very hard, and it may be worth it to spend a couple minutes thinking about it.
- Insertion: decide how many lists will this node be a part of. With a probability of 1/2, make the node a part of the lowest-level list only. With 1/4 probability, the node will be a part of the lowest two lists. With 1/8 probability, the node will be a part of three lists. And so forth. Insert the node at the appropriate position in the lists that it is a part of.
- Deletion: remove the node from all sorted lists that it is a part of.
- Check if contains: we can use the O(log N) algorithm similar described above on multi-level lists.
And, all of these operations are pretty simple to implement in O(log N) time!
Source code
Here is a sample C# implementation for a skip list of integers:
class IntSkipList { private class Node { public Node[] Next { get; private set; } public int Value { get; private set; } public Node(int value, int level) { Value = value; Next = new Node[level]; } } private Node _head = new Node(0, 33); // The max. number of levels is 33 private Random _rand = new Random(); private int _levels = 1; /// <summary> /// Inserts a value into the skip list. /// </summary> public void Insert(int value) { // Determine the level of the new node. Generate a random number R. The number of // 1-bits before we encounter the first 0-bit is the level of the node. Since R is // 32-bit, the level can be at most 32. int level = 0; for (int R = _rand.Next(); (R & 1) == 1; R >>= 1) { level++; if (level == _levels) { _levels++; break; } } // Insert this node into the skip list Node newNode = new Node(value, level + 1); Node cur = _head; for (int i = _levels - 1; i >= 0; i--) { for (; cur.Next[i] != null; cur = cur.Next[i]) { if (cur.Next[i].Value > value) break; } if (i <= level) { newNode.Next[i] = cur.Next[i]; cur.Next[i] = newNode; } } } /// <summary> /// Returns whether a particular value already exists in the skip list /// </summary> public bool Contains(int value) { Node cur = _head; for (int i = _levels - 1; i >= 0; i--) { for (; cur.Next[i] != null; cur = cur.Next[i]) { if (cur.Next[i].Value > value) break; if (cur.Next[i].Value == value) return true; } } return false; } /// <summary> /// Attempts to remove one occurence of a particular value from the skip list. Returns /// whether the value was found in the skip list. /// </summary> public bool Remove(int value) { Node cur = _head; bool found = false; for (int i = _levels - 1; i >= 0; i--) { for (; cur.Next[i] != null; cur = cur.Next[i]) { if (cur.Next[i].Value == value) { found = true; cur.Next[i] = cur.Next[i].Next[i]; break; } if (cur.Next[i].Value > value) break; } } return found; } /// <summary> /// Produces an enumerator that iterates over elements in the skip list in order. /// </summary> public IEnumerable<int> Enumerate() { Node cur = _head.Next[0]; while (cur != null) { yield return cur.Value; cur = cur.Next[0]; } } }
Possible improvements
- Obviously, a more useful implementation would be generic, so that we can store values other than integers.
- Nodes can be structs instead of classes. This significantly reduces the number of heap allocations. But, we cannot use the null value anymore to represent the tail, which adds a bit of extra code.
- The skip list could be made associative, so that each node stores a key/value pair.
- The implementation I gave above is a multiset. It is pretty simple to change the skip list so that it implements a set instead.
Related:
- Original paper on skip lists [umd.edu]
- Skip list [wikipedia.com]
- Quicksort killer [igoro.com]
- Programming job interview challenge [igoro.com]
Tags: Algorithms
Man, that is really interesting! I’m going to have to dig into that a bit more later. Oh, and nice blog!
here you go:
public class SkipList : ICollection where T : IComparable
{
private struct SkipListNode
{
private readonly N item;
private readonly SkipListNode?[] next;
public SkipListNode(N item, int depth)
{
this.item = item;
next = new SkipListNode?[depth];
}
public N Item
{
get { return item; }
}
public SkipListNode?[] Next
{
get { return next; }
}
}
private int count = 0;
private int depth = 1;
private SkipListNode head = new SkipListNode(default(T), 33);
public bool Contains(T item)
{
SkipListNode cur = head;
for (int level = depth – 1; level >= 0; level–)
{
for (; cur.Next[level] != null; cur = cur.Next[level].Value)
{
if (cur.Next[level].Value.Item.CompareTo(item) > 0)
{
break;
}
if (cur.Next[level].Value.Item.CompareTo(item) == 0)
{
return true;
}
}
}
return false;
}
public bool Remove(T item)
{
SkipListNode cur = head;
bool found = false;
for (int level = depth – 1; level >= 0; level–)
{
for (; cur.Next[level] != null; cur = cur.Next[level].Value)
{
if (cur.Next[level].Value.Item.CompareTo(item) == 0)
{
found = true;
cur.Next[level] = cur.Next[level].Value.Next[level];
count–;
break;
}
if (cur.Next[level].Value.Item.CompareTo(item) > 0)
{
break;
}
}
}
return found;
}
public void Add(T item)
{
// Determine the new depth of this new node. Retrieve the hashcode for value. The number of
// 1-bits before we encounter the first 0-bit is the level of the node. Since hashcode is
// 32-bit, the level can be at most 32.
int nodeLevel = 0;
for (int hash = item.GetHashCode(); (hash & 1) == 1; hash >>= 1)
{
nodeLevel++;
if (nodeLevel == depth)
{
depth++;
break;
}
}
// Insert this node into the skip list
SkipListNode newNode = new SkipListNode(item, nodeLevel + 1);
SkipListNode cur = head;
for (int level = depth – 1; level >= 0; level–)
{
for (; cur.Next[level] != null; cur = cur.Next[level].Value)
{
if (cur.Next[level].Value.Item.CompareTo(item) > 0)
{
break;
}
}
if (level <= nodeLevel)
{
newNode.Next[level] = cur.Next[level];
cur.Next[level] = newNode;
count++;
}
}
}
public void Clear()
{
head = new SkipListNode(default(T), 33);
count = 0;
}
public void CopyTo(T[] array, int arrayIndex)
{
throw new NotImplementedException();
}
public int Count
{
get { return count; }
}
public bool IsReadOnly
{
get { return false; }
}
private IEnumerator GetTheEnumerator()
{
SkipListNode? cur = head.Next[0];
while (cur != null)
{
yield return cur.Value.Item;
cur = cur.Value.Next[0];
}
}
public IEnumerator GetEnumerator()
{
return GetTheEnumerator();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
return GetTheEnumerator();
}
}
[...] Skip lists are fascinating! – Igor Ostrovsky takes a look at a list data structure known as Skip Lists – interesting reading [...]
Minor update: count++ in method Add needs to be moved two lines below.
BTW: The initial filling for a skiplist is nicely distributed, but i’m curious to find out what happens when many Add / Remove operations are used. Will the list remain still as efficient? What will happen to the depth used?
And my implementation relies on GetHashCode in combination with IComparable, i don’t know if that’s a correct assumption to make. It works for ints, since GetHashCode returns the same int value. If i recall correct, there is no such restraint for the values returned by GetHashCode. I think it will be better to avoid the problem, by not relying on IComparable at all.
I’ve made a different version of this list, which implements a Set (only unique items are added in the list, no duplicates). This works lightning fast.
BTW: IMHO the durations for linked lists are on average O(N/2), not O(N)
In the best case scenario the item is in front of the list, in the worst case scenario the last item is retrieved, on average the desired item is located somewhere in the middle of the list.
I’ve tested skiplist, list and hashtable, here are the results:
Testing SkipList vs List vs Hashtable, using 100000 items
[SkipList]
– Insertions : 455378
– Contains : 1005696
– Remove : 1480769
[List]
– Insertions : 8798
– Contains : 146389620
– Remove : 171897388
[HashTable]
– Insertions : 106101
– Contains : 160336
– Remove : 228002
I don’t see difference between skip list and binary tree without rebalancing operations. Is skip list more effective or not?
AlexR: A skip list is like a balanced tree. At least, it is like a balanced tree with an extremely high probability.
How does skip list do that? These two properties ensure it:
1. About 1/2 of nodes are in the lowest list only, about 1/4 nodes are in the lowest two lists, 1/8 in the lowest three, and so forth.
2. Nodes with different “heights” are mixed up about evenly.
After any sequence of insertions and removals, properties (1) and (2) still hold.
You can define these properties much more precisely, and use them to prove that insertion, removal and lookup are O(log N) on a skip list, with a very high probability.
Makes sense?
Remco:
Wow, seems like you looked at skip lists pretty in depth! Awesome, experimentation is a great way to learn. Here are responses to some of your points:
- The “distribution” of nodes: see answer to AlexR I just posted.
- GetHashCode: if two values are equal, then their hash codes are guaranteed to be equal. But, hash codes are not intended for less-than-greater-than comparison, and don’t work that way in general.
- O(N) vs O(N/2): it is true that in a sorted list, a lookup will visit N/2 nodes on average. In the big-Oh notation, O(N) is the same as O(N/2), and it is customary to drop the constant factor of 1/2.
- Note that a skip list is an ordered data structure, so it can do a number of things efficiently that a hash table cannot: e.g. in-order enumeration, find the smallest element larger than X, etc.
- When running your benchmarks, make sure you are measuring a RELEASE build rather than a DEBUG build.
Hope that helps, and thanks for reading.
@Igor: Agreed. Benchmarking was done in release mode (debugging takes to long to run
). The Hashtable is faster in inserts and removals, in-order iteration is not be supported by an hashtable (order is not gauranteed / used).
One last note on ‘my’ implementation: i think it’s better (in general) to restore the randon number generation instead of using the hashcode to determine the depth of the node. Using hashcodes in case of integers will generate a nice distribution, but for all other types all bets are off
Requiring where T : IComparable on the list is desirable.
(i just noticed that the type parameters in my sample are missing, just the better, this will prevent viewers from using it as-is, with all the known defects
)
Nice article! I wrote an article on skip lists a while back you might find interesting. It has links to a lecture available on iTunes from MIT that covers skip lists in some detail as well:
http://tech.puredanger.com/2007/10/03/skip-lists/
You should really also check out the ConcurrentSkipListMap included in Java 6:
http://java.sun.com/javase/6/d.....stMap.html
One of the big benefits of skip lists is that because they are built around linked lists, they can exhibit very localized locking. ConcurrentSkipListMap is a concurrent skip list based map and is written in lock free style (no synchronization, relies solely on CAS-like operations). This makes ConcurrentSkipListMap a concurrent sorted map with excellent performance. I’d recommend reading the source code as well as it is extremely well written and a great example of lock-free coding.
[...] Skip Lists Are Fascinating: Igor Ostrovsky takes a look at the skip list, a simple, yet powerful data structure. [...]
I like it!!!!
I like this type of data structure for it’s simplicity and efficiency. Keep going with this kind of articles they’re very useful. Thanks
In fact all this information + sample code was posted on on MSDN a while ago.
?
Do the guys in MS use MSDN
Linked lists:
http://msdn.microsoft.com/en-u.....S.80).aspx
Other data structures (queue, stack, BT, BST, etc.):
http://msdn.microsoft.com/en-u.....S.80).aspx
@Pablo: Ah, cool. I didn’t know about the MSDN article.
My approach to explaining skip lists is significantly different from the explanation in the MSDN article, and there are differences in the implementation as well.
So, I wouldn’t say that my post is redundant.
[...] Skip lists are fascinating! [...]
[...] skip over nodes. For a detailed description of how skip lists work and a C# implementation, see my earlier article on skip [...]
[...] Skip list are fascinating! [...]
[...] Skip list are fascinating! [...]