Imagine that 90,000 years ago, every man alive at the time picked a different last name. Assuming that last names are inherited from father to son, how many different last names do you think there would be today?
It turns out that there would be only one last name!
Similarly, imagine that 200,000 years ago, every woman alive picked a different secret word, and told the secret word to her daughters. And, the female descendants would follow this tradition – a mother would always pass her secret word to her daughters.
As you might guess, today there would be only one secret word in circulation.
The man whose last name all men would carry is called “Y-chromosomal Adam” and the woman whose secret word all women would know is “Mitochondrial Eve”. The names come from the fact that Y chromosome is a piece of DNA inherited from father to son (just like last names), and mitochondrial DNA is inherited from mother to children (just like the hypothetical secret words).
Why the convergence?
So, how likely is it that one last name and one secret word will eventually come to dominate? Given enough time, it is virtually guaranteed, under some assumptions (e.g., the population does not become separated).
Here is a simulation of how last names of five men could flow through six generations:
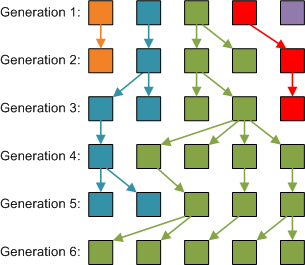
After six generations, the last name shown as green is the only last name around, purely by chance! In biology, this random effect is called genetic drift.
And, the convergence does not only happen for small populations. Here are the numbers that I got by simulating different population sizes:
| Population | Generations to convergence |
| 10 | 23 |
| 50 | 73 |
| 100 | 239 |
| 500 | 891 |
| 1000 | 1395 |
| 5000 | 7312 |
| 10000 | 13491 |
Here is the implementation of this simulation:
static int MitochondrialEve(int populationSize) { Random random = new Random(); int generations = 0; int[] cur = new int[populationSize]; for (int i = 0; i < populationSize; i++) cur[i] = i; for ( ; cur.Max() != cur.Min(); generations++) { int[] next = new int[populationSize]; for (int i = 0; i < next.Length; i++) { next[i] = cur[random.Next(populationSize)]; } cur = next; } return generations; }
This simulation is not a sophisticated model of a human population, but it is sufficient for the purposes of illustrating genetic drift. It assumes that every man has on average one son, with a standard deviation of roughly one, and a binomial probability distribution.
By the way, the Y-chromosomal Adam lived roughly 60,000–90,000 years ago, while Eve lived roughly 200,000 years ago. The reason why genetic drift acted faster for men is that men have a larger variation in the number of offspring – one man can have many more children than one woman.
UPDATE: Based on comments at Hacker News and Reddit, some readers are dissatisfied with the assumption of a fixed population size. Of course, human population grew over the ages, but there were also periods when it shrank, sometimes a lot. For example, roughly 70,000 years ago, the human population may have dropped down to thousands of individuals (1, 2). So, a fixed population size is a reasonable simplification for my example.
The roles of Mitochondrial Eve and Y-chromosomal Adam
One noteworthy fact about Mitochondrial Eve and Y-chromosomal Adam is that their positions in the history are not as special as they may first appear. Let’s take a look at this in more depth.
Tracing from me, I can follow a path of paternal ancestry all the way to Y-chromosomal Adam:

If I only trace the male ancestry, there is exactly one path that starts at me, and that path leads to Y-chromosomal Adam. You could start the diagram at any man alive today and you’d get a similar picture, with the lineage finally reaching the Y-chromosomal Adam.
However, if I trace ancestry via both parents, the number of ancestors explodes. I have two parents, four grandparents, eight great grandparents, and so forth. The number of ancestors in each generation grows exponentially, although that cannot continue for long. If all ancestors in each generations were distinct, I would have more than 1 billion ancestors just 30 generations back, so the tree certainly has to start collapsing into a directed acyclic graph by then.
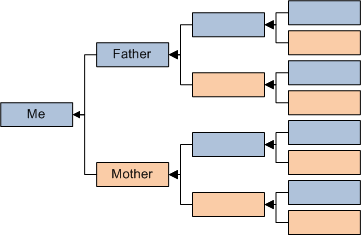
Tracing ancestry through both parents, there are many paths to follow, and each generation of ancestors contains a lot of people. Some of those paths will reach Y-chromosomal Adam, but other paths will reach other men in his generation. Similarly, some paths will reach Mitochondrial Eve, but other paths will reach other women in her generation.
Most recent common ancestor
So, Mitochondrial Eve only has a special position with respect to the mother-daughter relationships, and Y-chromosomal Adam only with respect to the father-son relationships.
What if you consider all types of ancestry, father-son, father-daughter, mother-son and mother-daughter? In the resulting directed acyclic graph, neither the Y-chomosomal Adam nor the Mitochondrial Eve appear in a special position. In fact, in the combined graph, the most recent ancestor of all today’s people lived much later than Y-chromosomal Adam. The most recent ancestor is estimated to have lived roughly 15,000 to 5,000 years ago.
One way to visualize the relationship between Mitochondrial Eve, Y-chromosomal Adam, and the Most Recent Common Ancestor (MRCA) is to look at a small genealogy diagram with just a few people:
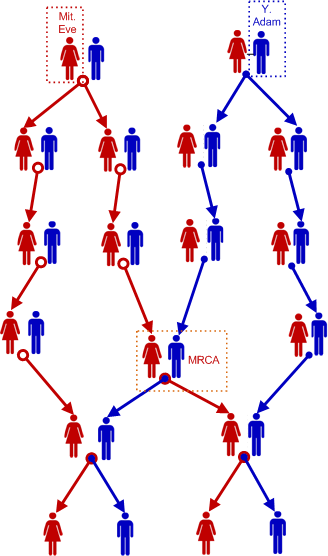
For the last generation consisting of just four people, this graph shows the Mitochondrial Eve, the Y-chromosomal Adam, and the most recent common ancestors (a couple in this example, but could also be one man or one woman). Adam is at the root of the blue tree, Eve is at the root of the red tree, and the most recent common ancestors are much lower in the graph.
The dating of Y-Adam and M-Eve
Finally, I’ll briefly give you an idea on how biologists calculate when Mitochondrial Eve and Y-chromosomal Adam lived.
The dating is based on DNA analysis. Changes in DNA accumulate at a certain rate that depends on various factors – region of the DNA, the species, population size, etc. To date Mitochondrial Eve, biologists calculate an estimate of the mitochondrial DNA (mtDNA) mutation rate. Then, they look at how much mtDNA varies between today’s women, and then calculate how long it would take to achieve that degree of variation.
Another interesting fact is that the titles of Mitochondrial Eve and Y-chromosomal Adam are not permanent, but instead are reassigned over time. For example, the woman who we call “Mitochondrial Eve” today did not hold that title during her lifetime. Instead, there was another unknown woman who was the most recent common matrilineal ancestor of all women alive at Eve’s time.
Final words
I hope you enjoyed the article. I originally learned about Y-chromosomal Adam and Mitochondrial Eve from reading Before the Dawn, and immediately knew I had to blog about them from a programmer’s perspective. If you want to read more on the topic, the Wikipedia page on Mitochondrial Eve is a good start.
Read more of my articles:
Fast and slow if statements: branch prediction in modern processors
Human heart is a Turing machine, research on XBox 360 shows. Wait, what?
Self-printing Game of Life in C#
And if you like my blog, subscribe!

Excellent. Really interesting, well-written article!
This model assumes that the population size is constant.
My greatly simplified example does assume a constant population size. But, a constant population size is not a requirement for genetic drift.
Besides, the human population fluctuated in the past, sometimes dropping to small numbers. For example, roughly 70,000 years ago, the human population may have dropped down to thousands of individuals (1, 2).
I’ll add a clarification to the article, since the same point was raised on Hacker News and reddit as well.
> But, a constant population size is not a requirement for genetic drift.
Certainly it isn’t. But it does disqualify the model from being “not an awful one”.
OK, I rephrased it:
Is that better?
Hi Igor. You might be interested in the following theorem, which I’ve submitted to the journal Cladistics and is awaiting peer review right now. Assume mankind doesn’t go extinct; that everyone has one male parent and one female parent; that mankind traces back to one ultimate pair of ancestors; and that no individual has infinitely many children. Then: there is an infinite subset X of people such that 1. every parent of a person in X is also in X, and 2. every member of X is an ancestor of all-but-finitely-many of the members of X.
[Edit: nevermind, I misread “all-but-finitely-many” as “finitely many”]
Xamuel: I don’t follow. Mitochondrial Eve is an (non-unique) ancestor to all people alive today. So, only a finite number of people will ever exist that were not descended from Eve.In order for X to be infinite, an infinite number of Eve’s descendants must be in X. Then clearly also Eve must be in X.
But then Eve is an ancestor to infinitely many members of X, which contradicts (2).