Over the past couple of years, auto-complete has popped up all over the web. Facebook, YouTube, Google, Bing, MSDN, LinkedIn and lots of other websites all try to complete your phrase as soon as you start typing.
Auto-complete definitely makes for a nice user experience, but it can be a challenge to implement efficiently. In many cases, an efficient implementation requires the use of interesting algorithms and data structures. In this blog post, I will describe one simple data structure that can be used to implement auto-complete: a ternary search tree.
Trie: simple but space-inefficient
Before discussing ternary search trees, let’s take a look at a simple data structure that supports a fast auto-complete lookup but needs too much memory: a trie. A trie is a tree-like data structure in which each node contains an array of pointers, one pointer for each character in the alphabet. Starting at the root node, we can trace a word by following pointers corresponding to the letters in the target word.
Each node could be implemented like this in C#:
class TrieNode { public const int ALPHABET_SIZE = 26; public TrieNode[] m_pointers = new TrieNode[ALPHABET_SIZE]; public bool m_endsString = false; }
Here is a trie that stores words AB, ABBA, ABCD, and BCD. Nodes that terminate words are marked yellow:
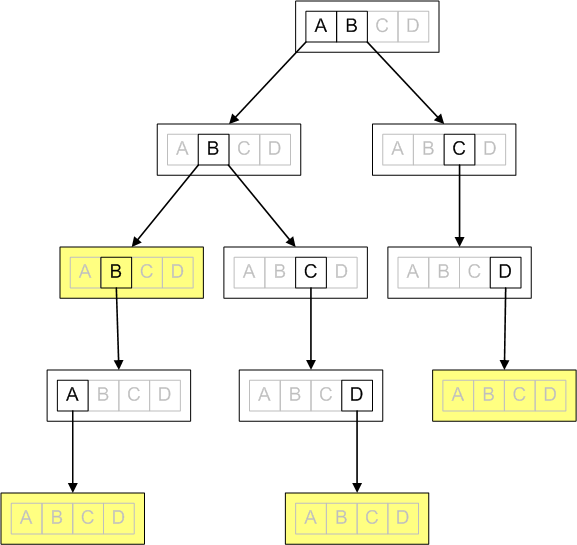
Implementing auto complete using a trie is easy. We simply trace pointers to get to a node that represents the string the user entered. By exploring the trie from that node down, we can enumerate all strings that complete user’s input.
But, a trie has a major problem that you can see in the diagram above. The diagram only fits on the page because the trie only supports four letters {A,B,C,D}. If we needed to support all 26 English letters, each node would have to store 26 pointers. And, if we need to support international characters, punctuation, or distinguish between lowercase and uppercase characters, the memory usage grows becomes untenable.
Our problem has to do with the memory taken up by all the null pointers stored in the node arrays. We could consider using a different data structure in each node, such as a hash map. However, managing thousands and thousands of hash maps is generally not a good idea, so let’s take a look at a better solution.
Ternary search tree to the rescue
A ternary tree is a data structure that solves the memory problem of tries in a more clever way. To avoid the memory occupied by unnecessary pointers, each trie node is represented as a tree-within-a-tree rather than as an array. Each non-null pointer in the trie node gets its own node in a ternary search tree.
For example, the trie from the example above would be represented in the following way as a ternary search tree:
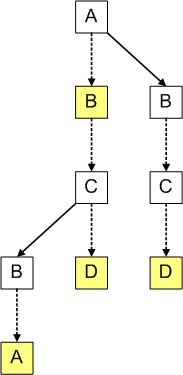
The ternary search tree contains three types of arrows. First, there are arrows that correspond to arrows in the corresponding trie, shown as dashed down-arrows. Traversing a down-arrow corresponds to “matching” the character from which the arrow starts. The left- and right- arrow are traversed when the current character does not match the desired character at the current position. We take the left-arrow if the character we are looking for is alphabetically before the character in the current node, and the right-arrow in the opposite case.
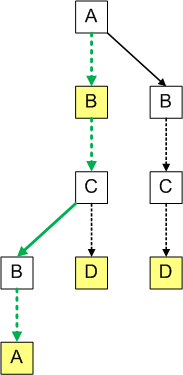
For example, green arrows show how we’d confirm that the ternary tree contains string ABBA:
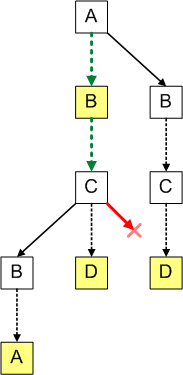
And this is how we’d find that the ternary string does not contain string ABD:
Ternary search tree on a server
On the web, a significant chunk of the auto-complete work has to be done by the server. Often, the set of possible completions is large, so it is usually not a good idea to download all of it to the client. Instead, the ternary tree is stored on the server, and the client will send prefix queries to the server.
The client will send a query for words starting with “bin” to the server:
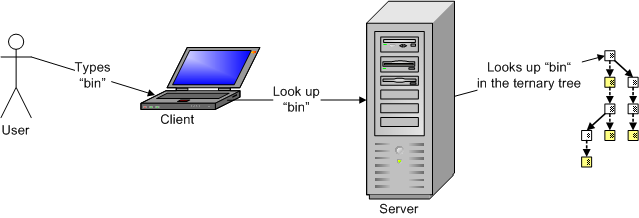
And the server responds with a list of possible words:
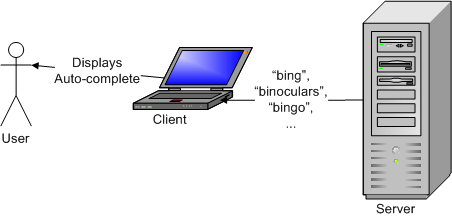
Implementation
Here is a simple ternary search tree implementation in C#:
public class TernaryTree { private Node m_root = null; private void Add(string s, int pos, ref Node node) { if (node == null) { node = new Node(s[pos], false); } if (s[pos] < node.m_char) { Add(s, pos, ref node.m_left); } else if (s[pos] > node.m_char) { Add(s, pos, ref node.m_right); } else { if (pos + 1 == s.Length) { node.m_wordEnd = true; } else { Add(s, pos + 1, ref node.m_center); } } } public void Add(string s) { if (s == null || s == "") throw new ArgumentException(); Add(s, 0, ref m_root); } public bool Contains(string s) { if (s == null || s == "") throw new ArgumentException(); int pos = 0; Node node = m_root; while (node != null) { int cmp = s[pos] - node.m_char; if (s[pos] < node.m_char) { node = node.m_left; } else if (s[pos] > node.m_char) { node = node.m_right; } else { if (++pos == s.Length) return node.m_wordEnd; node = node.m_center; } } return false; } }
And here is the Node class:
class Node { internal char m_char; internal Node m_left, m_center, m_right; internal bool m_wordEnd; public Node(char ch, bool wordEnd) { m_char = ch; m_wordEnd = wordEnd; } }
Remarks
For best performance, strings should be inserted into the ternary tree in a random order. In particular, do not insert strings in the alphabetical order. Each mini-tree that corresponds to a single trie node would degenerate into a linked list, significantly increasing the cost of lookups. Of course, more complex self-balancing ternary trees can be implemented as well.
And, don’t use a fancier data structure than you have to. If you only have a relatively small set of candidate words (say on the order of hundreds) a brute-force search should be fast enough.
Further reading
Another article on tries is available on DDJ (careful, their implementation assumes that no word is a prefix of another):
http://www.ddj.com/windows/184410528
If you like this article, also check out these posts on my blog:
Tags: Algorithms

Interesting.
What if you want to allow infix matching too?
ie “bin” matches “binoculars”, but also “rubbish bin” or “the bin bins”
The generalised suffix tree algorithm can match on a substring in a set of strings: http://en.wikipedia.org/wiki/G.....uffix_tree
But, if you want to allow infix matching, you may also want to support typo-correction, match ranking based on “closeness” to what you typed, match ranking based on popularity of different words, etc.
I would imagine that say Google uses some crazy data structures that account for all of these factors. But then if you are a site like Google, nothing is ever simple.
I think this is only usefull if you’re also going to modify the trie a lot. If it’s just a relatively static serverside tree for autocompletions, an ordered table and binary search would be much more efficient, or else a compressed trie
It’s worth pointing out that tries and structures similar to them have issues with case preserving but case insensitive operations. Consider the shape for sequences like:
aBcd
aBdd
abbd
abcd
… and then find all items with the prefix “abc”, considered case-insensitively.
Case preserving but insensitive comparisons normally sort uppercase characters directly before their corresponding lower-case characters, but the way tries store the data, they must either (1) normalize and lose the case data, failing the preservation requirement, or (2) store each letter case separately and have much greater difficulty finding all elements with the same prefix (considered case insensitively), as items with the same prefix may exist in multiple descendants and an in-order traversal of the trie will place the items out of lexicographical order.
Somejan & Barry: Both very good points. As is usual, the list of caveats and alternate solutions should be a lot longer than the actual article.
Barry: A reasonable solution to the casing problem would be to store the list of properly cased words in each terminal node. If words rarely differ by casing only (as is probably the case in practice), the list would typically be of length 1, maybe 2.
[…] Efficient auto-complete with a ternary search tree | Igor Ostrovsky Blogging (tags: tree search strings ui) […]
Igor: one reason for using a trie (especially a Patricia trie) for lookup of strings with lots of common prefixes is that it can be far more space-efficient than e.g. a sorted array used with binary search. Storing the full, properly-cased string in the terminal nodes negates this advantage.
Why not just use a full-text search index like lucene?
Barry: You could save space by storing the casing as a bitmask rather than a string. Still, even that is some extra space.
Seide: I am not familiar with lucene. Either way, this article is more about explaining a cool data structure than about giving the most practical solution for auto-complete.
If ternary tree structure like the above pictrue,words seq should be “AB”,”ABCD”,”ABBA” & “BCD”.
alex, it may look like “AB” is in the diagram, but really it is just “A”. A letter only counts if you follow a down-arrow that starts from that letter.
[…] Efficient auto-complete with a ternary search tree […]
Igor: If you want to support nearest match, the easiest thing to do is to store and search against lexemes (say, metaphone or soundex or whatever). If you want, you can take the Levenstein difference between the potential string and the source string as a quick sort criterion for small matches; it wouldn’t scale, though, since you’d have to apply it to every source string available.
For larger matching that scales on machines with a fair amount of memory available, the easiest way to deal with it is to knock out one lexeme from the word at a time, and match the gap with a GADDAG or something.
Also, a suffix trie is a rather simpler way to resolve this quandry you’re approaching.
Great post! Nice!
Excellent story once again! Thumbs up:)
Perhaps your ternary search tree is incorrect? ABBA should be one straight branch. I have re written this here :
http://techpanacea.blogspot.co.....trees.html
A. Shiraz: That depends on the order of insertions. If ABBA was inserted before ABCD then yes, ABBA would be one straight branch.
ok I assumed that was the order of insertion implied in the text.
AB, ABBA, ABCD, and BCD.
Fair enough. When I made that diagram, I was only thinking about making sure that the tree in the diagram holds the right strings. I didn’t think about making the tree consistent with the implied insertion order.
Contains(string) will return if the word is there in tree or not
How will autocomplete work??
i.e How will you generate the list of all words with prefix s(string) ?
Can you suggest any iterative or recursive method for same
Ternary Search Tree is cool. I have just released a key-value data store based on Ternary Search Tree. Here is the URL: http://code.google.com/p/tstdb/
if insert strings like,ab, bc,cd,de,ef,fg,ha,iaaa… I think the right branch is like a list, like, a->b->c->d->e->f->i. Searching a string is rather slow.
great work! thanks!
but can this be ajusted to support top-k query?
Hey Igor, nice article. I was wondering if the data structure you have on your server is persistent between client requests ? That is, you are not constructing a data structure in each and every client request. If that is indeed the case, how did you achieve Data structure persistence ?
For full picture you can add 2 more methods here that make tries (or TSTs) very powerful:
1. String matching using wildcards.
2. Longest prefix search.
Here is the missing autocomplete function
public List AutoComplete(String s)
{
if (s == null || s == "") throw new ArgumentException();
List suggestions = new List();
int pos = 0;
Node node = m_root;
while (node != null)
{
int cmp = s[pos] - node.m_char;
if (s[pos] node.m_char) { node = node.m_right; }
else
{
if (++pos == s.Length)
{
if (node.m_wordEnd == true)
{
suggestions.Add(s);
}
FindSuggestions(s, suggestions, node.m_center);
return (suggestions);
}
node = node.m_center;
}
}
return (suggestions);
}
private void FindSuggestions(string s, List suggestions, Node node)
{
if (node == null)
{
return;
}
if (node.m_wordEnd == true)
{
suggestions.Add(s + node.m_char);
}
FindSuggestions(s, suggestions, node.m_left);
FindSuggestions(s + node.m_char, suggestions, node.m_center);
FindSuggestions(s, suggestions, node.m_right);
}
Hi,
I have found this code very useful. It wouldn’t have been my first choice for quick lookup, but it suited well to a map site i have just spun up.
The missing autocomplete function requires a few more mods to get it operational (Did anyone else spot the mistakes !!) Included below is updated code, which stores the original cased string and also a termID which allows my client sided map to automatically zoom and render a tile for that particular area of interest.
Thanks Igor for taking the time to publish this. The autocomplete client sided jquery i used was devbridge. Also included is code which renders out the correct JSON object for devbridge (https://github.com/devbridge/jQuery-Autocomplete). As for the caching the Trie object, any persistance mechanism for asp.net will suffice.
namespace COMMON.Trees
{
public class Node
{
internal char m_char;
internal Node m_left, m_center, m_right;
internal bool m_wordEnd;
internal string m_cased = null;
internal int m_termId;
public Node(char ch, bool wordEnd)
{
m_char = ch;
m_wordEnd = wordEnd;
}
}
public class TernaryTree
{
public Node m_root = null;
void Add(string s, int pos, ref Node node, string preservedCase, int termID)
{
if (node == null) { node = new Node(s[pos], false); }
if (s[pos] node.m_char) { Add(s, pos, ref node.m_right, preservedCase, termID); }
else
{
if (pos + 1 == s.Length)
{
node.m_wordEnd = true;
node.m_cased = preservedCase;
node.m_termId = termID;
}
else { Add(s, pos + 1, ref node.m_center, preservedCase, termID); }
}
}
public void Add(string toAdd, int termID)
{
if (toAdd == null || toAdd == “”) throw new ArgumentException();
Add(toAdd.ToLower(), 0, ref m_root, toAdd, termID);
}
bool Contains(string s)
{
if (s == null || s == “”) throw new ArgumentException();
int pos = 0;
Node node = m_root;
while (node != null)
{
int cmp = s[pos] – node.m_char;
if (s[pos] node.m_char) { node = node.m_right; }
else
{
if (++pos == s.Length) return node.m_wordEnd;
node = node.m_center;
}
}
return false;
}
public List AutoComplete(String toMatch)
{
if (toMatch == null || toMatch == “”)
throw new ArgumentException();
toMatch = toMatch.ToLower();
List _suggestionValues = new List();
List _suggestionPoints = new List();
int pos = 0;
Node node = m_root;
while (node != null)
{
// get the
int cmp = toMatch[pos] – node.m_char;
if (toMatch[pos] != node.m_char)
{
// mo match,
if (cmp < 0)
node = node.m_left;
else
node = node.m_right;
}
else
{
if (++pos == toMatch.Length)
{
if (node.m_wordEnd == true)
{
// suggestions.Add(s); gives you the lowercased
_suggestionValues.Add(node.m_cased);
_suggestionPoints.Add(node.m_termId);
}
FindSuggestions(toMatch, _suggestionValues,_suggestionPoints, node.m_center);
return (_suggestionValues);
}
node = node.m_center;
}
}
return (_suggestionValues);
}
void FindSuggestions(string s, List suggestions, List suggestionPoints, Node node)
{
if (node == null)
{
return;
}
// eg: “an” is as string,
if (node.m_wordEnd == true)
{
// suggestions.Add(s + node.m_char); // gives you the lower cased
suggestions.Add(node.m_cased);
suggestionPoints.Add(node.m_termId);
}
FindSuggestions(s, suggestions,suggestionPoints, node.m_left); // A
FindSuggestions(s + node.m_char , suggestions,suggestionPoints, node.m_center);
FindSuggestions(s, suggestions,suggestionPoints, node.m_right); // when out results in “qq palais-sur-vienne”
// results: when A and B removed, then no results returned.
}
}
}
StringBuilder _response = new StringBuilder();
_response.Append(“{ \”query\” :\”” + _queryID + “\”, \”suggestions\” :[“);
bool _first = true;
foreach (string r in _completions)
{
if (!_first)
_response.Append(“,”);
_response.Append(“{ \”value\”: \”” + r + “\”, \”data\”: \”” + r + “\” }”);
_first = false;
}
Dear Sir,
Your Article is very nice and it is a nice way to implement searching. But Please if you have then send me a c# implementation code. I need that as I want to implement this.
Whats your email Abhishek Kumar ?
[…] Efficient auto-complete with a ternary search tree […]
Hi Igor,
a question about TrieNode class. How we can branch from the “B” in the second level node under “A” to have words “ABBA” and “ABCD”?
What is the largest set of data, like number of long string rows have you tested this on? Anything more than 1 million?
please give a java source code for dictionary with autospell cheker
the future and it is time to be happy. I’ve read this post and if I could I want to suggest you some
Skype has launched its website-based customer beta for the world, after launching it broadly in the United states and U.K.
before this four weeks. Skype for Web also now works with Chromebook and Linux for instant messaging interaction (no voice and
video yet, all those demand a plug-in installment).
The increase of your beta adds assist for an extended list of dialects to help strengthen that overseas user friendliness